viernes, 28 de agosto de 2015
viernes, 10 de julio de 2015
Gráfico vectorial
De Wikipedia, la enciclopedia libre
Saltar a: navegación, búsqueda

Locomotora a vapor en formato de imagen vectorial, originalmente en formato Windows Metafile, WMF (convertido a PNG.) Se puede comprobar que a la imagen le falta realismo fotográfico en comparación con su equivalente en formato matricial o rasterizado.
Este es un ejemplo en el que se pueden comparar los gráficos vectoriales (columna de la izquierda) con los gráficos rasterizados (columna de la derecha) al ampliar las respectivas imágenes. Como se puede comprobar, a medida que aumenta el zoom los gráficos de la izquierda mantienen su calidad, mientras que los de la derecha van revelando paulatinamente los píxeles que conforman la imagen. Los gráficos vectoriales pueden ser escalados ilimitadamente sin perder su calidad. Los dos ejemplos de ampliación al 300% y al 600% ilustran especialmente bien esta propiedad de los gráficos vectoriales: los contornos de las figuras geométricas (franjas blancas detrás de la letra A) no aumentan proporcionalmente en la figura en el caso del gráfico rasterizado.
Este formato de imagen es completamente distinto al formato de las imágenes de mapa de bits, también llamados imágenes matriciales, que están formados por píxeles. El interés principal de los gráficos vectoriales es poder ampliar el tamaño de una imagen a voluntad sin sufrir la pérdida de calidad que sufren los mapas de bits. De la misma forma, permiten mover, estirar y retorcer imágenes de manera relativamente sencilla. Su uso también está muy extendido en la generación de imágenes en tres dimensiones tanto dinámicas como estáticas.
Todos los ordenadores actuales traducen los gráficos vectoriales a mapas de bits para poder representarlos en pantalla al estar ésta constituida físicamente por píxeles.
Historia
Desde los inicios del computador en 1950 hasta la década de los ochenta se usaba un sistema vectorial de generación de gráficos diferente al actual. En este sistema «caligráfico» el rayo electrónico del tubo de rayos catódicos de la pantalla era guiado directamente para dibujar las formas necesarias, segmento de línea por segmento de línea, quedando en negro el resto de la pantalla. Este proceso se repetía a gran velocidad para alcanzar una imagen libre de intermitencias o muy cercana a estar libre de ellas. Este sistema permitía visualizar imágenes estáticas y en movimiento de buena resolución (para esas fechas) sin usar la inimaginable cantidad de memoria que se hubiera necesitado para conseguir la resolución equivalente en un sistema de rasterización, permitiendo que la secuencia de imágenes diese la sensación de movimiento e incluso consiguiendo que titilaran modificando sólo algunas de las palabras del código de la gráfica en su respectivo display file. Estos monitores basados en vectores también eran conocidos como monitores X-Y (X-Y displays).Uno de los primeros usos de los vectores en el proceso de visualización fue el realizado por la Fuerza Aérea de los Estados Unidos. El sistema de generación de gráficos mediante vectores se utilizó hasta 1999 en el control aéreo y probablemente aún se siga usando en diversos sistemas militares. Ivan Sutherland empleó este mismo sistema en la TX-2 para ejecutar su programa Sketchpad en el MIT Lincoln Laboratory en 1963.
Los subsiguientes sistemas de representación gráfica vectorial incluían la GT40 de Digital; existió una consola llamada Vectrex que usaba gráficos vectoriales para mostrar videojuegos como Asteroids y Space Wars; y equipos como el Tektronix 4014, podían generar imágenes vectoriales dinámicas.
El término vector es usado comúnmente en el contexto de gráficos de dos dimensiones producidos por computador. Es uno de los muchos modos con los que un artista cuenta para crear una imagen con una previsualización rasterizada. Otras formas de uso pueden ser en textos, en multimedia y en la creación de escenarios 3D. Prácticamente todos los programas de modelado en 3D usan técnicas que generan gráficos vectoriales en 2D. Los plotters usados en dibujo técnico siguen dibujando los vectores directamente sobre el papel
Imagen de mapa de bits
Color
Cada punto representado en la imagen debe contener información de color, representada en canales separados que representan los componentes primarios del color que se pretende representar, en cualquier modelo de color, bien sea RGB, CMYK, LAB o cualquier otro disponible para su representación. A esta información, se puede sumar otro canal que representa la transparencia respecto al fondo de la imagen. En algunos casos, (GIF) el canal de transparencia tiene un solo bit de información, es decir, se puede representar como totalmente opaco o como totalmente transparente; en los más avanzados (PNG, TIFF), el canal de transparencia es un canal con la misma profundidad del resto de canales de color, con lo cual se pueden obtener centenares, miles o incluso millones de niveles de transparencia distintos.Resolución
Sin embargo, existe una fórmula matemática que permite definir esta resolución según el sustrato de impresión:
lpp x 2 x f a/r = ppp
Donde lpp (líneas por pulgada) es la lineatura a utilizarse según el sustrato, por ejemplo: 150 lpp, si son papeles recubiertos, 85 lpp para periódico, etc.
2 es un factor basado en la capacidad de rasterización del escanner
y f a/r es la ampliación o disminución en que se necesita la imagen.
La fórmula puede utilizarse solamente como lpp x 2 = ppp.
Conversión entre mapas de bits y gráficos vectoriales
La transformación de un mapa de bits a un formato vectorial se llama vectorización. Este proceso normalmente se lleva a cabo o bien manualmente (calcando el mapa de bits con curvas de Bézier o polígonos vectoriales) o bien con ayuda de un programa específico, como por ejemplo Corel PowerTrace o Inkscape. El proceso inverso, convertir una imagen vectorial en una imagen de mapa de bits, es mucho más sencillo y se llama rasterización.
El cubo de Rubik es un cuerpo tridimensional que podemos «interpretar» como un cuerpo formado por vóxeles, la versión tridimensional de un píxel.
Analogía en 3D
En infografía 3D (tres dimensiones) el concepto de una rejilla plana de píxeles se extiende a un espacio tridimensional formado por ladrillos cúbicos llamados vóxeles. En este caso, existe una reja tridimensional con elementos (cubitos) que contienen la información del color. A pesar de que los vóxeles son un concepto potente para tratar cuerpos con formas complejas exigen mucha memoria para ser almacenados. En consecuencia, a la hora de producir imagénes en tres dimensiones se utilizan más a menudo imágenes vectoriales 3D.DIFERENCIA ENTRE UNA IMAGEN VECTORIAL Y UNA DE MAPA DE BITS.
Mejor respuesta: En el mapa de bits la imagen se divide en pequeños puntos de color, donde cada color es representado por una combinación de 3 números (en el formato mas usado, RGB). Por eso se llama mapa de bits. Cuantos más puntos tengamos para representar una imagen, esta se verá mejor y con mas detalle, y se dice que tiene mejor resolución.
Debido a esta característica es que resulta sencillo almacenar cualquier imagen en este formato, ya sea un paisaje o un dibujo, en especial si tenemos en cuenta que los métodos de captura de imagen o video son punto a punto, técnicamente hablando, a través de una matriz de sensores que capturan información de cada punto de la imagen. La cantidad de puntos depende exclusivamente del equipo capturador (camara de fotos, de video, etc) o sea de la resolución en la que está configurado o es capáz de reproducir.
Su dificultad principal es que una imagen exige resolución para ser vista con detalle y esto implica una mayor cantidad de puntos por imagen, o sea, mayor cantidad de bits. Por eso los mapas de bits no son buenos para dibujos, porque una linea inclinada, por ejemplo, se ve en realidad como una escalera si la resolución no es alta.
Un ejemplo, una imagen relativamente pobre de 640*480 implica una cantidad de 307200 puntos. Cada punto es un color definido que se representa por 3 números (3 bytes), uno para cada color basico Rojo-Verde-Azul, que combinados en distinta intensidad nos da una gama de colores suficiente para representar casi cualquier color sensible al ojo humano. Pero esta pobre imagen requiere 307200*3 o sea 921600 bytes, casi 1 MByte. De allí surge la necesidad de la compresión, usándose técnicas como JPEG o el PNG.
En resúmen (para lo que sigue), la imagen de un mapa de bits es un objeto único con miles de bytes de información.
En la imagen por vectores, la imagen es dibujada a partir de una superposición de figuras sencillas mediante tabla de funciones complejas y parámetros que modifican los resultados de esas funciones. Por esta razón es que resultan útiles para imagenes sencillas basadas en figuras geométricas principalmente (dibujos).
Debido a que la imagen se re-dibuja cada vez que se la utiliza, no exige resolución, ya que cambiando los parámetros podemos escoger cualquier tamaño en cualquier momento, lo que resulta en un ahorro sustancial de bytes. Sin embargo este método fracasa al intentar dibujar una imagen real, (un paisaje, por ejemplo), ya que necesitaría miles de figuras geométricas superpuestas para conseguirlo.
De Wikipedia, la enciclopedia libre.
Mejor respuesta: En el mapa de bits la imagen se divide en pequeños puntos de color, donde cada color es representado por una combinación de 3 números (en el formato mas usado, RGB). Por eso se llama mapa de bits. Cuantos más puntos tengamos para representar una imagen, esta se verá mejor y con mas detalle, y se dice que tiene mejor resolución.
Debido a esta característica es que resulta sencillo almacenar cualquier imagen en este formato, ya sea un paisaje o un dibujo, en especial si tenemos en cuenta que los métodos de captura de imagen o video son punto a punto, técnicamente hablando, a través de una matriz de sensores que capturan información de cada punto de la imagen. La cantidad de puntos depende exclusivamente del equipo capturador (camara de fotos, de video, etc) o sea de la resolución en la que está configurado o es capáz de reproducir.
Su dificultad principal es que una imagen exige resolución para ser vista con detalle y esto implica una mayor cantidad de puntos por imagen, o sea, mayor cantidad de bits. Por eso los mapas de bits no son buenos para dibujos, porque una linea inclinada, por ejemplo, se ve en realidad como una escalera si la resolución no es alta.
Un ejemplo, una imagen relativamente pobre de 640*480 implica una cantidad de 307200 puntos. Cada punto es un color definido que se representa por 3 números (3 bytes), uno para cada color basico Rojo-Verde-Azul, que combinados en distinta intensidad nos da una gama de colores suficiente para representar casi cualquier color sensible al ojo humano. Pero esta pobre imagen requiere 307200*3 o sea 921600 bytes, casi 1 MByte. De allí surge la necesidad de la compresión, usándose técnicas como JPEG o el PNG.
En resúmen (para lo que sigue), la imagen de un mapa de bits es un objeto único con miles de bytes de información.
En la imagen por vectores, la imagen es dibujada a partir de una superposición de figuras sencillas mediante tabla de funciones complejas y parámetros que modifican los resultados de esas funciones. Por esta razón es que resultan útiles para imagenes sencillas basadas en figuras geométricas principalmente (dibujos).
Debido a que la imagen se re-dibuja cada vez que se la utiliza, no exige resolución, ya que cambiando los parámetros podemos escoger cualquier tamaño en cualquier momento, lo que resulta en un ahorro sustancial de bytes. Sin embargo este método fracasa al intentar dibujar una imagen real, (un paisaje, por ejemplo), ya que necesitaría miles de figuras geométricas superpuestas para conseguirlo.
De Wikipedia, la enciclopedia libre.
Debido a esta característica es que resulta sencillo almacenar cualquier imagen en este formato, ya sea un paisaje o un dibujo, en especial si tenemos en cuenta que los métodos de captura de imagen o video son punto a punto, técnicamente hablando, a través de una matriz de sensores que capturan información de cada punto de la imagen. La cantidad de puntos depende exclusivamente del equipo capturador (camara de fotos, de video, etc) o sea de la resolución en la que está configurado o es capáz de reproducir.
Su dificultad principal es que una imagen exige resolución para ser vista con detalle y esto implica una mayor cantidad de puntos por imagen, o sea, mayor cantidad de bits. Por eso los mapas de bits no son buenos para dibujos, porque una linea inclinada, por ejemplo, se ve en realidad como una escalera si la resolución no es alta.
Un ejemplo, una imagen relativamente pobre de 640*480 implica una cantidad de 307200 puntos. Cada punto es un color definido que se representa por 3 números (3 bytes), uno para cada color basico Rojo-Verde-Azul, que combinados en distinta intensidad nos da una gama de colores suficiente para representar casi cualquier color sensible al ojo humano. Pero esta pobre imagen requiere 307200*3 o sea 921600 bytes, casi 1 MByte. De allí surge la necesidad de la compresión, usándose técnicas como JPEG o el PNG.
En resúmen (para lo que sigue), la imagen de un mapa de bits es un objeto único con miles de bytes de información.
En la imagen por vectores, la imagen es dibujada a partir de una superposición de figuras sencillas mediante tabla de funciones complejas y parámetros que modifican los resultados de esas funciones. Por esta razón es que resultan útiles para imagenes sencillas basadas en figuras geométricas principalmente (dibujos).
Debido a que la imagen se re-dibuja cada vez que se la utiliza, no exige resolución, ya que cambiando los parámetros podemos escoger cualquier tamaño en cualquier momento, lo que resulta en un ahorro sustancial de bytes. Sin embargo este método fracasa al intentar dibujar una imagen real, (un paisaje, por ejemplo), ya que necesitaría miles de figuras geométricas superpuestas para conseguirlo.
De Wikipedia, la enciclopedia libre.
lunes, 16 de marzo de 2015
La función SI en Excel
La función SI en Excel es parte del grupo de funciones Lógicas y nos permite evaluar una condición para determinar si es falsa o verdadera. La función SI es de gran ayuda para tomar decisiones en base al resultado obtenido en la prueba lógica.Sintaxis de la función SI
Además de especificar la prueba lógica para la función SI también podemos especificar valores a devolver de acuerdo al resultado de la función.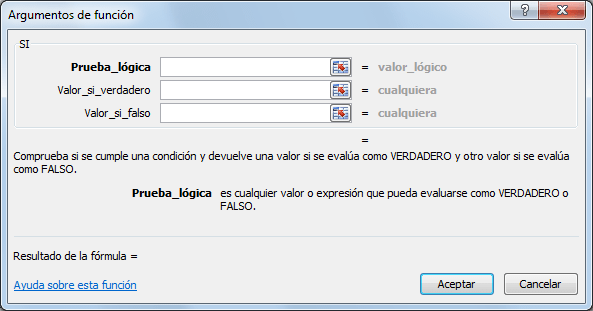
- Prueba_lógica (obligatorio): Expresión lógica que será evaluada para conocer si el resultado es VERDADERO o FALSO.
- Valor_si_verdadero (opcional): El valor que se devolverá en caso de que el resultado de la Prueba_lógica sea VERDADERO.
- Valor_si_falso (opcional): El valor que se devolverá si el resultado de la evaluación es FALSO.
Los argumentos Valor_si_verdadero y Valor_si_falso pueden ser cadenas de texto, números, referencias a otra celda o inclusive otra función de Excel que se ejecutará de acuerdo al resultado de la Prueba_lógica.
Ejemplos de la función SI
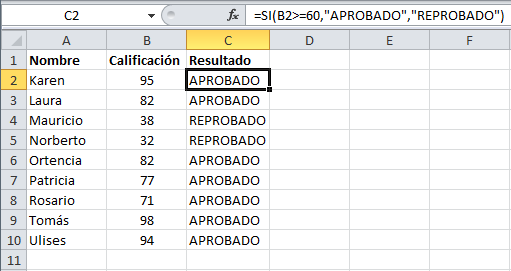
Probaremos la función SI con el siguiente ejemplo. Tengo una lista de alumnos con sus calificaciones correspondientes en la columna B. Utilizando la función SI desplegaré un mensaje de APROBADO si la calificación del alumno es superior o igual a 60 y un mensaje de REPROBADO si la calificación es menor a 60. La función que utilizaré será la siguiente:=SI(B2>=60,"APROBADO","REPROBADO")Observa el resultado al aplicar esta fórmula en todas las celdas de la columna C.
Utilizar una función como prueba lógica
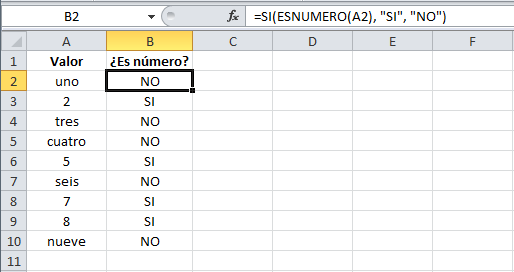
Es posible utilizar el resultado de otra función como la prueba lógica que necesita la función SI siempre y cuando esa otra función regrese como resultado VERDADERO o FALSO. Un ejemplo de este tipo de función es la función ESNUMERO la cual evalúa el contenido de una celda y devuelve el valor VERDADERO en caso de que sea un valor numérico. En este ejemplo quiero desplegar la leyenda “SI” en caso de que la celda de la columna A efectivamente tenga un número, de lo contrario se mostrará la leyenda “NO”.=SI(ESNUMERO(A2), "SI", "NO")Este es el resultado de aplicar la fórmula sobre los datos de la hoja:
Utilizar una función como valor de regreso
Como último ejemplo mostraré que es posible utilizar una función para especificar el valor de regreso. Utilizando como base el ejemplo anterior, necesito que en caso de que la celda de la columna A contenga un valor numérico se le sume el valor que colocaré en la celda D1. La función que me ayudará a realizar esta operación es la siguiente:=SI(ESNUMERO(A2), SUMA(A2, $D$1), "NO")Como puedes observar, el segundo argumento es una función la cual se ejecutará en caso de que la prueba lógica sea verdadera. Observa el resultado de esta fórmula:
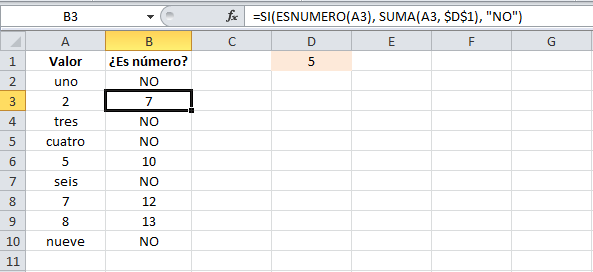
Sólo en los casos donde la función SI era verdadera se realizó la suma. De la misma manera podríamos colocar una función para el tercer argumento en caso de que el resultado de la prueba lógica fuera falso.
Suscribirse a:
Comentarios (Atom)


